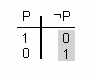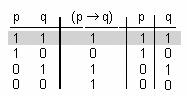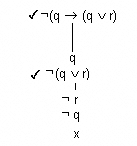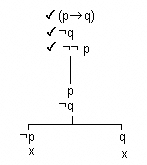Lògica

 (del grec λογική lógiké, derivat de logikós, que es refereix a la raó, de λόγος, logos, raó)

Ciència formal que estudia les formes dels raonaments ben fets.

És el procediment sistemàtic i fundat que ens permet diferenciar un raonament correcte, o vàlid d'un altre incorrecte, o invàlid. És, per aquesta raó, estudi de la deducció lògica o de la inferència lògica.

Pot també definir-se com l'estudi sobre la consistència dels enunciats que afirmem (veg. citació), o com la ciència de les regles que ens permeten usar correctament l'expressió «per tant», o un equivalent de la mateixa (veg. citació).

Argumentacions

Els següents paràgrafs són exemples d'argumentacions o raonaments

1. Sempre que s'acosta el Nadal Anna està contenta; estem ja a 20 de desembre; Per tant Anna està contenta.

2. Un cavall és un animal; per tant, el cap d'un cavall és el cap d'un animal (A de Morgan).

3. Cap persona honesta roba; ara bé, és sabut que alguns personatges cèlebres roben; per tant hi ha personatges cèlebres que no són honests.

4. Tinc ganes de descansar; per tant m'en vaig de viatge.

ja que són raonaments vàlids o correctes, els enunciats que es compon cadascun d'ells són consistents entre si, l'ocupació de l'expressió «per tant» o equivalent és legítima, i, en cada cas, la conclusió ha estat deduïda vàlidament de les premisses.

Perquè hi hagi un raonament, no cal que la disposició dels enunciats sigui la formal, la pròpia de la lògica; un raonament pot tenir també una disposició informal, com en l'exemple següent:

	Tots estem bojos per aquí. Jo estic boig; tu també ho estàs [...]
	"I com saps tu si jo estic boja?", li va preguntar Alicia.
	"Has d'estar-ho per força", li va contestar el Gat; "en cas contrari no hauries vingut aquí".
	Alicia va pensar que això no provava res; però va continuar de totes maneres: "I com saps que tu estàs boig?"
	"Per començar," va reposar el Gat, "els gossos no estan bojos, d'acord?".
	"Suposo que no", va reposar Alicia.
	"Bé, doncs llavors", va continuar dient el Gat, "veuràs que els gossos grunyen quan alguna cosa no els agrada, i mouen la cua quan estan contents.
	En canvi jo grunyo quan estic content i moc la cua quan m'enutjo.
	Per tant, estic boig"
	______________________________________________
	L. Carroll, Alicia al país de les meravelles, Aliança, Madrid 1983, p. 111.

També aquí la conclusió es dedueix correctament –vàlidament– de les seves premisses. No és aquest el cas, malgrat les aparences, del següent raonament:

Si vas al pol nord has d'abrigar-te bé

No vas al pol nord

Per tant no has d'abrigar-te bé

Raonament incorrecte ja que, el fet de no anar al pol nord no significa que no s'hagi d'anar a una altra zona freda on sigui necessari abrigar-se.

La correcció –o validesa– d'un argument no depèn que els enunciats que es compon siguin, de fet, veritables o falsos, sinó de si, entre premisses i conclusió, existeix conseqüència lògica. La lògica estudia la conseqüència lògica des d'un punt de vista formal, és a dir, no atenent a la veritat de fet dels enunciats, sinó a la forma com s'argumenta: si la forma d'argumentar és correcta, llavors, si les premisses són veritables, la conclusió serà també veritable. Trobar les formes correctes d'argumentar suposa trobar el criteri pel qual decidim que un raonament és vàlid o invàlid.

Veritat i validesa

Una cosa és que la conclusió sigui veritable i una altra que la seva deducció sigui vàlida. Una cosa és la veritat de les premisses i la conclusió, i una altra la validesa del raonament. Aquella depèn, segons la teoria de la correspondència, de si el que l'enunciat diu és, en realitat, el mateix que succeeix: aquesta, de si la conclusió és una conseqüència lògica de les premisses. La validesa depèn de la forma com s'argumenta i no del contingut de veritat o falsedat els seus enunciats.

Un enunciat és conseqüència lògica de les premisses si és impossible que les premisses siguin veritables i la conclusió falsa. Això depèn únicament de la forma del raonament i no de cap veritat de fet. Diem, doncs, que un raonament és vàlid -formalment correcte- quan la seva forma és tal que sempre que les premisses són veritables la conclusió també ho és, o bé quan és impossible que les premisses siguin veritables i la conclusió falsa. I sempre i en tot cas, la validesa d'un raonament no depèn de la veritat o falsedat de les premisses. Si el raonament és vàlid i, a més, les seves premisses són veritables, el raonament és també materialment correcte, això és, un raonament sòlid.

En els raonaments vàlids, les premisses impliquen la conclusió. I llavors, les premisses i la conclusió són necessàriament consistents.

També pot dir-se que un raonament és vàlid si el seu contraexemple fa de les premisses i de la conclusió un conjunt d'enunciats inconsistent.

En conclusió, només si raonem correctament, estem legitimats a utilitzar les expressions «per consegüent», «per tant» i d'altres equivalents.

Llenguatge formal

Per a estudiar la forma dels raonaments, la lògica recorre a llenguatges formals. El mateix Aristòtil, fundador de la lògica, va estudiar la forma dels sil·logismes mitjançant esquemes d'enunciats. Així, recorre a expressions formals com: «Tot A és B», «B pertany a tot A», o «B es predica de tot A». Amb el desenvolupament de la lògica moderna, anomenada «lògica simbòlica» o «lògica matemàtica» s'han creat formalismes lògics, llenguatges formals o càlculs lògics.

Un llenguatge formal permet representar mitjançant fórmules gairebé qualsevol expressió d'aquest mateix llenguatge, i amplia considerablement la capacitat de formalitzar –limitada a uns quants tipus d'enunciats, preferentment els categòrics– de la lògica clàssica aristotèlica, també anomenada lògica tradicional.

Un llenguatge formal s'identifica amb el conjunt de fórmules que poden formar-se seguint les seves regles: el conjunt de fórmules ben formades d'un llenguatge.

Tot llenguatge formal suposa:

1) un conjunt de símbols, que constitueixen el alfabet del llenguatge, i

2) un conjunt de regles de formació de fórmules.

Si s'afegeix una tercera condició, a saber,

3) un conjunt de regles de transformació d'unes fórmules en unes altres, s'obté, a més, un càlcul lògic o un procediment de deducció.

Un llenguatge formal o un càlcul lògic permet, en conseqüència, decidir:

1) si un símbol pertany al llenguatge;

2) si una fórmula determinada és una expressió ben formada del llenguatge; i

3) si una seqüència sintàctica de fórmules constitueix una demostració o una deducció.

En tot cas, un càlcul o un procediment de deducció posa de manifest que tot raonament vàlid equival a una expressió lògica que sempre és veritable. Una tal expressió és una «veritat lògica» o una «veritat formal».

La lògica d'enunciats i la lògica de predicats són dos llenguatges lògics formals. La distinció entre l'un i l'altre es basa en la diferent capacitat expressiva del llenguatge. Els símbols (alfabet) del llenguatge de lògica d'enunciats es refereixen, bàsicament, a enunciats i a connexions entre enunciats, deixant intacta la seva estructura interna, mentre que els símbols (alfabet) de la lògica de predicats penetren a l'interior dels enunciats i es refereixen als termes que es componen els enunciats.

1.«Quan surt el sol, clareja»

és una expressió de lògica d'enunciats, si d'ella ens interessa la relació, o connexió, que s'estableix entre les dues oracions simples, també anomenades atòmiques:

p = surt el sol

q = clareja

la relació «quan» se simbolitza mitjançant la connectiva «...si.... llavors» (formalment [math]\displaystyle{ (p\rightarrow{}q) }[/math]):

En canvi, el conjunt d'enunciats

2. «Tot el que creu en la igualtat humana creu en la democràcia

Els estudiants creuen en la igualtat humana

Per tant els estudiants creuen en la democràcia»

no quedaria prou representat si escrivíssim:

(p i q) per tant r

Per això, la lògica de predicats, analitza l'estructura interna d'aquests enunciats, i permet escriure (segons la lògica aristotèlica):

Tot A és B

Tot C és A

_________________

Per tant tot C és B

O bé segons la lògica simbòlica:

[math]\displaystyle{ \forall{x}(Px \rightarrow{}Qx) }[/math]

[math]\displaystyle{ \forall{x}(Rx \rightarrow{}Px) }[/math]

________________________________

[math]\displaystyle{ \forall{x}(Rx \rightarrow{}Qx) }[/math]

El sistema de la lògica elemental, o de primer ordre, es divideix en lògica d'enunciats i lògica de predicats.

Lògica d'enunciats

Un enunciat és tota oració gramatical declarativa, això és, aquella que és capaç de ser veritable o falsa, atès que tot enunciat expressa –o significa– una proposició. El principi de bivalència, un dels fonaments de la lògica clàssica, estableix a més que tot enunciat, o proposició, ha de ser veritable o fals, i no ambdues coses alhora. (La lògica d'enunciats també es coneix com a lògica proposicional, degut a la similitud entre enunciats i proposicions).

Els enunciats poden ser simples (atòmics) o compostos (moleculars) i se simbolitzen mitjançant lletres d'enunciat (p, q, r, s,... minúscules).

Els enunciats es combinen entre si mitjançant connectives lògiques, també anomenades operadors (perquè operen entre enunciats) o juntors. Per això la lògica d'enunciats també es coneix com lògica de connectors o lògica de juntors). Els principals connectors són: "no", "i", "o", "si..., llavors", "si i només si", i en símbols

[math]\displaystyle{ ¬, \wedge, \vee, \to, \leftrightarrow }[/math]

El llenguatge formal de la lògica d'enunciats consta de:

1. Símbols

a) Lletres d'enunciat: p, q, r, s... (variables d'enunciat)

b) Operadors o connectors (o connectives) [math]\displaystyle{ ¬, \wedge, \vee, \to, \leftrightarrow }[/math] (Constants)

c) Elements auxiliars com (...), [...]

2. Regles de formació de fórmules

a. Tota lletra d'enunciat és una fórmula ben formada (fbf) del llenguatge, i constitueix un enunciat simple

b. Si P és una fbf, també ho és ¬P

c. Si [math]\displaystyle{ P }[/math] i [math]\displaystyle{ Q }[/math] són fbf, també ho són

[math]\displaystyle{ (P\wedge Q), (P\vee Q), (P\to Q), (P\leftrightarrow{Q}) }[/math]Els símbols i les fórmules constitueixen la sintaxi del llenguatge formal i, amb aquesta definició recursiva de fórmula, és possible decidir què expressió pertany a aquest llenguatge i expressar una quantitat indefinida d'enunciats.

Exemple

No qualsevol successió de símbols és una fórmula ben formada, o una expressió del llenguatge. Així, per exemple,

no són fórmules:

[math]\displaystyle{ p ¬q r }[/math], per 2,3

mentre que són fórmules

[math]\displaystyle{ p\wedge¬q }[/math], per 2,2

[math]\displaystyle{ ¬p\vee¬q }[/math], per 2,2

[math]\displaystyle{ \neg (p \leftrightarrow q) }[/math], per 2,1

Però un llenguatge formalitzat no consta només d'una sintaxi (a saber, símbols i regles de formació de fórmules), sinó també d'una semàntica: ha de poder ser interpretat (ha de referir-se a alguna cosa). Interpretar un llenguatge és atribuir significat a les seves constants (símbols) i a les seves variables (lletres d'enunciats). El significat que se li atribueix és el valor de veritat.

A tot enunciat descriptiu de caràcter empíric, li assignem un valor de veritat concret -sabem si és veritable o fals- segons la seva correspondència amb els fets que descriu; a un enunciat lògic, la referència del qual als fets s'ignora metodològicament, només podem assignar-li valors de veritat possibles:

Així, a tota lletra d'enunciat se li assignen dos valors possibles: V i F (1, 0)

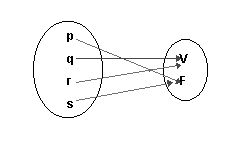
Una assignació de valors de veritat és una aplicació d'un conjunt de lletres d'enunciat (argument: p, q, r, s...) a un conjunt de valors de veritat (valor: V, F). Apliquem a cada lletra d'enunciat un sol valor de veritat V (1) o de falsedat F (0).

En aquesta figura, a p se li assigna el valor F, a q el valor V, a r el valor V i a s el valor F.

Una assignació és una interpretació. Una interpretació és, per tant, una aplicació o una funció que assigna a una fórmula, o expressió de lògica d'enunciats, els seus possibles valors de veritat. El nombre d'assignacions per cada

Per a una lletra d'enunciat,

p [math]\displaystyle{ =2^{1} }[/math]

p = 1, p =0.

Per a dues lletres d'enunciat,

p,q [math]\displaystyle{ =2^{2} }[/math]

p = 1 i q = 1

p = 1 i q = 0

p = 0 i q = 1

p = 0 i q = 0

Per a tres lletres d'enunciat,

p, q, r [math]\displaystyle{ =2^{3} }[/math]

p = 1, q = 1 i r = 1

p = 1, q = 1 i r = 0

p = 1, q = 0 i r = 1

p = 1, q = 0 i r = 0

p = 0, q = 1 i r = 1

p = 0, q = 1 i r = 0

p = 0, q = 0 i r = 1

p = 0, q = 0 i r = 0

Per a n lletres d'enunciat,

n [math]\displaystyle{ =2^{n} }[/math]

A partir de la noció d'assignació de valors és possible definir cadascuna de les connectives com a operadors veritativo-funcionals, perquè, aplicades a un enunciat simple (quan es tracta de ¬) o a dos enunciats simples (en els altres casos), donen un valor de veritat de l'enunciat compost que és funció del valor dels enunciats que el componen. Per aquesta raó les connectives es defineixen de la següent manera:

Connectives

«Una connectiva veritativo-funcional és una constant lògica que expressa una manera determinada d'interpretar el valor de veritat d'un enunciat compost a partir del valor de veritat dels components.»

La lògica defineix cadascuna d'aquestes maneres mitjançant una [#tablasdeverdad taula de veritat] pròpia de cada connectiva.

ja que no interessa el valor de veritat segons el contingut material dels enunciats, s'utilitzen lletres d'enunciats (lletres minúscules; p, q, r,...) en lloc d'enunciats (i per a parlar de les lletres d'enunciats s'utilitzen també lletres, aquesta vegada, majúscules: P, Q, R,..., anomenades variables metalingüístiques).

Negació [math]\displaystyle{ \neg P }[/math]

«”No P” és fals quan P és veritable i és veritable quan P és fals»

Exemple

Si és veritat que p («fa sol»), ¬p és fals («no fa sol» és fals)

Si és fals que p (és fals que «fa sol»), ¬p és veritable («no fa sol»)

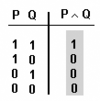
Conjunció [math]\displaystyle{ P\wedge Q }[/math]

«”P i Q” ([math]\displaystyle{ P\wedge Q }[/math])és veritable només quan els seus enunciats components, P i Q són tots dos veritables».

Exemple

Si p = "fa fred" i q = "fa vent", la fórmula [math]\displaystyle{ P\wedge Q }[/math] ("fa fred i vent") és veritable solament si és veritat que "fa fred" i és veritat que "fa vent", en cualquir un altre cas és falsa.

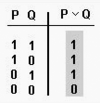
Disjunció [math]\displaystyle{ P\vee Q }[/math]

«”P o Q” és veritable quan és veritable P o quan és veritable Q, o ho són tots dos alhora».

Exemple

Si p = «Anna és bona» i q = «Anna sembla bona», l'enunciat «Anna és bona o ho sembla» és veritat si resulta que és bona o si només ho sembla, o si és bona i, a més, ho sembla.

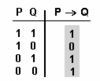
Condicional [math]\displaystyle{ P\rightarrow{}Q }[/math]

«”Si P, llavors Q” és veritable sempre, menys quan l'antecedent, P, sigui veritable i el conseqüent, Q, fals».

Exemple:

Si algú diu: p = "Anna estudia, q = "Anna aprova", la fórmula [math]\displaystyle{ p\rightarrow{}q }[/math], que llegeix "si Anna estudia, aprova" (o "Si Anna estudis, entoces aprova") és veritable en els casos següents:

Anna estudia i aprova

Anna no estudia però aprova

Anna ni estudia ni aprova

Solament és fals l'enunciat si Anna estudia però no aprova.

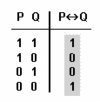
Bicondiconal [math]\displaystyle{ P \leftrightarrow Q }[/math]

«”P si i només si Q” és veritable quan P i Q són tots dos veritables o tots dos falsos; en els altres casos, és fals».

Exemple

Si p = ets feliç» i q = «estimes», l'enunciat «ets feliç si i només si mestresses», o «ets feliç sempre que estimis» és veritat quan «ets feliç i mestresses» i quan «ni ets feliç ni mestresses», però és fals si és veritat una d'ambdues coses i no l'altra.

Altres connectives possibles

El nombre de funcions de veritat possibles (N) respon a la fórmula combinatòria

[math]\displaystyle{ N=m^{^{m^{n}}} }[/math]

on n és el nombre de lletres d'enunciat i m els valors de veritat (V i F) i m, com a nombre base, les dues combinacions possibles del valor global de V i F per a cada assignació. Per a una expressió lògica de dues lletres d'enunciat,

[math]\displaystyle{ N=2^{^{2^{2}}} }[/math]

per tant, per a dos enunciats, p i q, les funcions de veritat possibles són 16. Cadascuna de les columnes de la següent taula són les seves definicions.

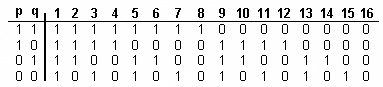
Cadascuna d'aquestes columnes descriu una possible funció de veritat, segons la fórmula esmentada; les columnes 9-16 són la negació de la seva simètrica en les columnes 8-1, per aquest ordre. Les columnes 2, 5, 7, i 8 són les usuals funcions de veritat definides (disjunció, condicional, bicondicional i conjunció), i la 11 i la 13, la negació (de q i de p, respectivament).

columna 1: tautologia [math]\displaystyle{ (p\vee ¬p)\wedge (q \vee ¬q) }[/math]	columna 2: disjunció inclusiva [math]\displaystyle{ (p\vee q) }[/math]
columna 3: condicional material inversa [math]\displaystyle{ (q\rightarrow p) }[/math]	columna 4: afirmació de p [math]\displaystyle{ (p) }[/math]
columna 5: condicional material [math]\displaystyle{ (p\rightarrow q) }[/math]	columna 6: afirmació de q [math]\displaystyle{ (q) }[/math]
columna 7: bicondicional [math]\displaystyle{ (p\leftrightarrow q) }[/math]	columna 8: conjunció [math]\displaystyle{ (p\wedge q) }[/math]
columna 9: incompatibilitat (p/q) Barra o functor de Scheffer [math]\displaystyle{ (¬p\vee ¬q), ¬(p\wedge q), o (p\rightarrow ¬q) }[/math]	columna 10: disjunció exclusiva [math]\displaystyle{ p\veebar q }[/math]
columna 11: negació de q [math]\displaystyle{ (¬q) }[/math]	columna 12: afirmació de q i negació de p [math]\displaystyle{ ¬(q\rightarrow p)= (q\wedge ¬p) }[/math]
columna 13: negació de p [math]\displaystyle{ (¬p) }[/math]	columna 14: afirmació de q i afirmació de p [math]\displaystyle{ ¬(p\rightarrow q)= (p\wedge ¬q) }[/math]
columna 15: [math]\displaystyle{ (p\downarrow q) }[/math] negació de la disjunció, o functor de Peirce [math]\displaystyle{ ¬(p\vee q), (¬p\wedge ¬q) }[/math] "solament és veritable si tots dos enunciats són falsos"	columna 16: contradicció [math]\displaystyle{ (p\wedge ¬p)\vee (q\wedge ¬q) }[/math]

Nota: Les funcions expressades en les columnes 9 i 15 (functor de Sheffer i functor de Peirce, respectivament) es consideren connectives adequades: elles soles poden representar totes les restants.

(Repetim la mateixa taula de valors per a poder visualitzar adequadament l'explicació de cada columna)

Taules de veritat

Algorisme que permet demostrar si una expressió de lògica d'enunciats és o no una fórmula lògicament veritable.

La noció de funció de veritat, que permet crear taules de tots els possibles valors de veritat d'una fórmula, permet també analitzar el de qualsevol expressió de lògica d'enunciats. Per això, una taula de veritat és també un mètode o procediment semàntic que:

1) Permet decidir si una fórmula és una tautologia, una contradicció, o una expressió consistent, i si dues o més fórmules són lògicament equivalents. I en connexió amb això, en el cas que tot raonament formalment vàlid és una tautologia -una implicació sempre veritable-

2) permet decidir si una seqüència d'enunciats, o de fórmules de lògica d'enunciats, constitueix un raonament vàlid.

Fórmules tautològiques

Una fórmula és una tautologia si és veritable per a qualsevol assignació de valors de veritat. En una taula de veritat, la tautologia dóna sempre valors veritables.

• Exemple

Donat l'enunciat

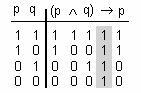
[math]\displaystyle{ (p\wedge q)\rightarrow p }[/math]

la seva taula de veritat és

El valor final és sempre vertader (1); és, per tant, una tautologia.

Fórmules contradictòries

Una fórmula és contradictòria si és falsa per a qualsevol assignació de valors de veritat.

• Exemple

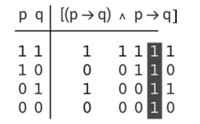
Donat l'enunciat condicional

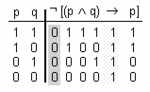
[math]\displaystyle{ ¬[(p\wedge q)\rightarrow p] }[/math]

la seva taula de veritat és

El seu valor final de veritat és fals (0)

Fórmules consistents

Una fórmula és consistent si hi ha almenys una assignació que la fa veritable; si no és, per tant, ni tautològica ni contradictòria.

Exemple

Donat l'enunciat condicional

[math]\displaystyle{ (p\wedge q) \rightarrow (q \wedge r) }[/math]

la seva taula de veritat és

No és, doncs, ni una tautologia ni una contradicció, atès que, segons els valors assignats, és veritable o fals.

Fórmules equivalents

Dues fórmules són equivalents si les assignacions de valors que fan veritable a una d'elles fan també veritable a l'altra, i viceversa, i si les assignacions de valors que fan falsa a una d'elles fan també falsa a l'altra, i viceversa.

Les taules de dues fórmules equivalents són iguals.

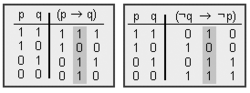
Exemple

Donades les fórmules

[math]\displaystyle{ (p \rightarrow q }[/math]) i [math]\displaystyle{ (¬q \rightarrow ¬p) }[/math]

les seves taules són

Ambdues fórmules són equivalents, i el valor final de les seves taules és el mateix.

Les taules permeten, a més, comprovar la conseqüència lògicai permeten també comprovar la independència lògica entre enunciats o fórmules

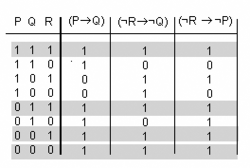
Exemple de comprovació de conseqüència lògica

Sigui [math]\displaystyle{ (P\rightarrow{}Q), (¬R\rightarrow{}¬Q), \models (¬R\rightarrow{}¬P)? }[/math]

la taula de veritat prova que [math]\displaystyle{ (¬R\rightarrow{}¬P) }[/math]

és una consecuenia lògica del comjunto [math]\displaystyle{ \Delta }[/math] de fórmules

[math]\displaystyle{ [(P\rightarrow{}Q), (¬R\rightarrow{}¬Q) }[/math]

ja que tota interpretació que fa verdader al conjunt [math]\displaystyle{ \Delta }[/math] fa també veritable la fórmula [math]\displaystyle{ (¬R\rightarrow{}¬P) }[/math]

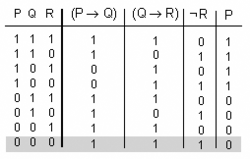
Exemple de comprovació d'independència lògica entre enunciats o fórmules

Siguin els enunciats [math]\displaystyle{ (P\rightarrow{}Q), (Q\rightarrow{}R), ¬R, \models P? }[/math].

La taula de veritat prova que l'enunciat P és independent de la resta d'enunciats.

Raonaments vàlids

Amb les nocions introduïdes fins aquí, es disposa ja d'un llenguatge formalitzat, amb el qual és possible expressar qualsevol raonament de lògica d'enunciats; és suficient indicar els mètodes que decideixen quines són les seqüències de fórmules que representen un raonament vàlid. Sobre aquestes seqüències de fórmules, és possible fer afirmacions de tipus semàntic, basades en l'atribució de la noció de veritat, o bé de tipus sintàctic, basades en la noció d'equivalència. Les primeres són pròpies dels mètodes semàntics, i les segones dels sintàctics.

Mètodes semàntics

1) Un raonament és vàlid si, sempre que les seves premisses són veritables, la conclusió també és veritable, i no és possible que, amb premisses veritables, la conclusió pugui ser falsa.

2) Un raonament vàlid és, en conseqüència, una implicació formalment vàlida. Pel mateix, un raonament és vàlid, si el seqüent semàntic que formen les seves premisses i la seva conclusió constitueix una tautologia.

Un seqüent és una afirmació (feta en metallenguatge) sobre un conjunt de fórmules lògiques (les premisses i la conclusió), utilitzant el signe de «conseqüència lògica». Per exemple, el conjunt [math]\displaystyle{ (p\rightarrow{}q), p \models q }[/math], on el signe [math]\displaystyle{ \models }[/math] significa "conseqüència lògica", pot representar a manera d'esquema el raonament següent:

«Si Anna somia, dorm

Anna està somiant,

__________________

per tant dorm»

del que s'afirma que si els dos primers enunciats són veritables, ho és també el tercer: que aquest se segueix lògicament dels altres dos.

Ús de taules

Dos són les maneres com podem utilitzar les taules per a demostrar la validesa d'un raonament.

Conseqüència lògica

Una fórmula, anomenada conclusió, és una conseqüència lògica d'una altra o unes altres, anomenades premisses, si tota interpretació –o assignació de valors de veritat– que fa veritables a les premisses fa també veritable a la conclusió:

Per a l'assignació de valors de la primera línia, es compleix que «la interpretació que fa veritable al conjunt de premisses fa també veritable a la conclusió».

Per tant, q és conseqüència lògica del conjunt donat de fórmules, com expressa el seqüent semàntic: [math]\displaystyle{ (p\rightarrow{}q), p \models q }[/math]

Implicació tautològica:

En el cas que sigui un raonament vàlid, l'exemple esmentat pot escriure's com una implicació: [math]\displaystyle{ [(p\rightarrow{}q)\wedge p]\rightarrow{}q }[/math]

La taula de veritat mostra que aquest condicional és una tautologia.

És una implicació veritable en tot cas, raó per la qual es compleix que «sempre que les premisses són veritables la conclusió també ho és, i en cap cas succeeix que les premisses siguin veritables i la conclusió falsa».

Per tant, tant per (1) com per (2), es mostra que el raonament és vàlid.

En resum, en un raonament vàlid hi ha conseqüència lògica entre premisses i conclusió: [math]\displaystyle{ A_1, A_2, ... A_n \models B }[/math]

O bé, si B és vàlid sense premisses: [math]\displaystyle{ \emptyset\models B }[/math]

La qual cosa significa simplement que B és una tautologia, o una fórmula universalment vàlida (vegeu llista de tautologies).

Arbres lògics

Aquest mètode anomenat també càlcul dels arbres lògics iniciat per I.W. Beth (1955), és un mètode semàntic que permet verificar si una fórmula és una tautologia o si una fórmula és una conseqüència lògica de les seves premisses, recorrent al concepte de consistència.

Permet demostrar tant que [math]\displaystyle{ \emptyset\models B }[/math], com que [math]\displaystyle{ A_1, A_2, ... A_n \models B }[/math]

Es demostra que [math]\displaystyle{ \models ¬B }[/math] és una contradicció (Exemple 1)

Sigui la tautologia [math]\displaystyle{ q\rightarrow{}(q\vee r) }[/math]. El seu arbre lògic és:

Per tant si [math]\displaystyle{ ¬q\rightarrow{}(q\vee r) }[/math] és una contradicció, [math]\displaystyle{ q\rightarrow{}(q\vee r) }[/math] és una tautologia.

,

o que el conjunt constituït per les premisses i la negació de la conclusió, que constitueix el seu contraexemple, [math]\displaystyle{ A_1, A_2, ... A_n \models ¬B }[/math] és inconsistent

Veure

Exemple 2

Sigui el conjunt de fórmules [math]\displaystyle{ (p\rightarrow{} q), ¬q \models ¬p }[/math], el seu arbre lògic és:

i

Exemple 3

Sigui el raonament següent: "Quan Anna canta, l'acompanya Raül o ho fa en Joel. Però avui no l'acompanya Raül, per tant, ja que en Joel tampoc l'acompanya, Anna no canta".

Que pot formalitzar-se de la següent manera: [math]\displaystyle{ [(p\rightarrow{}(q\vee r))\wedge ¬q]\rightarrow{}(¬r\rightarrow{}¬q) }[/math].

El seu arbre lògic és:

El conjunt format per les premisses donades i la negació de la conclusió (el contraexemple) és inconsistent; per tant el raonament és vàlid.

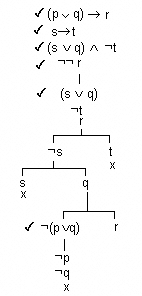
En canvi en el següent cas, el raonament no és vàlid.

Sigui [math]\displaystyle{ ((p\vee q)\rightarrow{}r), s\rightarrow{}t, ((s\vee q)\wedge ¬t), \vdash ¬r? }[/math]. El seu arbre lògic és:

La branca en què es troba [math]\displaystyle{ r }[/math] no està tancada; per tant, el conjunt format per les premisses i la negació de la conclusió no és inconsistent. Per tant el conjunt donat [math]\displaystyle{ ((p\vee q)\rightarrow{}r), s\rightarrow{}t, ((s\vee q)\wedge ¬t, \vdash ¬r? }[/math] és inconsistent, i la branca que queda sense tancar inclou els valors del contraexemple.

Prou una sola combinació de valors que facin inconsistent el conjunt perquè disposem d'un contraexemple que fa invàlid el raonament. (En aquest cas, p=0 o 1, q=1, r=1, s=0, t=0).

Vegeu la descripció del mètode en càlcul dels arbres lògics.

La noció lògica fonamental en els mètodes de taules és la de no contradicció o consistència entre premisses i conclusió. En els mètodes sintàctics la noció lògica fonamental és la d'equivalència entre fórmules que preserven, o transmeten, la veritat.

Mètodes sintàctics

Els mètodes sintàctics consisteixen a derivar o deduir una conclusió, a partir d'uns principis o unes premisses donades. Un raonament és, així, vàlid si la conclusió s'ha derivat o deduït correctament dels seus principis o premisses mitjançant regles; la validesa s'entén ara com deduïbilitat. En els mètodes semàntics, raonament vàlid és aquell que no admet la possibilitat que les seves premisses siguin veritables i la conclusió falsa; en els mètodes sintàctics és aquell la conclusió del qual s'ha demostrat, derivat o deduït correctament de principis o premisses (hipòtesis). La qual cosa s'expressa mitjançant el següent seqüent sintàctic: [math]\displaystyle{ A_1,A_2,...A_n \vdash B }[/math] que es llegeix "B es demostrava a partir de principis o premisses", o "B és deduïble", i on el signe [math]\displaystyle{ \vdash }[/math] representa la deduïbilitat de la fórmula B respecte d'una altra o unes altres. Si el conjunt de premisses és el conjunt buit, llavors [math]\displaystyle{ \emptyset\vdash B }[/math], o bé [math]\displaystyle{ \vdash B }[/math], i, en aquest cas, B és un teorema de la lògica. El teorema de la deducció (Herbrand, 1930) estableix que si [math]\displaystyle{ A_1, A_2, ... A_n \vdash B }[/math], llavors [math]\displaystyle{ \models A_1, A_2, ...A_n \rightarrow{} B }[/math], de manera que, si B es dedueix formalment a partir d'un conjunt de premisses, llavors la implicació que formen aquestes premisses i la conclusió B constitueixen una fórmula universalment vàlida.

a) Mètodes axiomàtics

El mètode més clàssic de deducció lògica. Un sistema formal axiomàtic es compon d'una llista d'axiomes i d'una o més regles d'inferència.

Qualsevol fórmula (B) d'aquesta seqüència és un teorema sintàctic [math]\displaystyle{ \vdash B }[/math] si es demostra a partir dels axiomes. Una demostració o derivació axiomàtica de B és:

1) una seqüència finita de fórmules

2) l'última fórmula del qual és B;

3) on cada fórmula és o un axioma o una conseqüència d'un axioma derivada mitjançant regles d'inferència.

Als sistemes axiomàtics, la característica general dels quals és, d'una banda, la simplicitat -tenen, comunament, poques regles d'inferència- i, per l'altre, la laboriositat de les demostracions (veg. exemple) segueixen, com a alternativa, a partir de 1934, els sistemes de deducció natural,ideats per G. Gentzen.

b) Deducció natural

Un dels sistemes formals de deducció, emprats en lògica, ideat independentment per Gerhard Gentzen (1909-1945), lògic i matemàtic alemany deixeble de Hilbert, i Stanislaw Jaskowsky, en 1934. Consisteix en un procediment de derivació per a provar la validesa d'una conclusió, partint de premisses inicials i deduint noves premisses intermèdies mitjançant regles d'inferència, l'ús de la qual es justifica. No recorre a axiomes i el procediment demostratiu en conjunt té certa semblança amb la manera «natural» de deduir.

Utilitza regles d'inferència per a cadascuna de les connectives i, com a pressupost fonamental, admet suposar com premissa qualsevol enunciat, que pot introduir-se condicionadament en qualsevol moment de la demostració (suposició que eventualment ha de cancel·lar-se recorrent a la demostració condicional o a la prova per reducció a l'absurd;

Exemple:

Pot demostrar-se, per exemple, que la fórmula [math]\displaystyle{ (P\wedge Q)\rightarrow{}Q }[/math] és un teorema de la lògica d'enunciats, que pot ser deduït sense recórrer a premisses:

1. [math]\displaystyle{ P\wedge Q }[/math] suposició

2. [math]\displaystyle{ Q }[/math] per eliminació del conjuntor en 1

3. [math]\displaystyle{ (P\wedge Q)\rightarrow{}Q }[/math] prova del condicional en 1 i 2

O també que [math]\displaystyle{ (P\rightarrow{}R) }[/math] és una conseqüència lògica de [math]\displaystyle{ (P\rightarrow{}Q) }[/math] i [math]\displaystyle{ (Q\rightarrow{}R) }[/math] raonant de la següent manera:

1. [math]\displaystyle{ P\rightarrow{}Q }[/math]

2. [math]\displaystyle{ Q\rightarrow{}R }[/math]

3. [math]\displaystyle{ P }[/math] suposició

4. [math]\displaystyle{ Q }[/math] MP 1,3

5. [math]\displaystyle{ R }[/math] MP 2,4

6. [math]\displaystyle{ P\rightarrow{}R }[/math] IC 3-5

raonament que és la justificació del «sil·logisme hipotètic».

Com a exemple de sistema de deducció natural utilitzem les vuit regles bàsiques de Gentzen i algunes de les derivades (Vegeu, per exemple, M. Garrido, Lògica simbòlica, Tecnos, Madrid 1983, p. 84 i p. 96-99.).

Veure les regles de Genzen

Usant aquestes regles Si es vol provar la validesa del següent raonament: [math]\displaystyle{ [(r\rightarrow{¬s})\wedge(p\rightarrow{r})\wedge p]\rightarrow{(¬s\vee t)} }[/math]

aplicant les regles bàsiques del càlcul de lògica d'enunciats,

es demostra que [math]\displaystyle{ (¬s\vee t) }[/math] és deduïble del conjunt de premisses [math]\displaystyle{ (r\rightarrow{}¬s), (p\rightarrow{}r), p }[/math]

Si es vol provar la validesa que [math]\displaystyle{ (p\rightarrow{¬s}) }[/math] és deduïble del conjunt de fórmules [math]\displaystyle{ (p\wedge s)\rightarrow{q}, (q\rightarrow{t}), (¬t\wedge s) }[/math], això és, [math]\displaystyle{ (p\wedge s)\rightarrow{q}, (q\rightarrow{t}), (¬t\wedge s) \vdash (p\rightarrow{¬s}) }[/math], aplicant regles bàsiques i derivades, s'obté:

Amb això es demostra que [math]\displaystyle{ [(p\wedge s)\rightarrow{q} \wedge (q\rightarrow{t}) \wedge (¬t\wedge s)]\rightarrow{}(p\rightarrow{¬s}) }[/math]

Conclusió

La lògica d'enunciats és un sistema formal que posseeix uns procediments de decisió efectius per a provar que una fórmula qualsevol és també una conseqüència lògica. Per tant constitueix un sistema formal decidible, ja que aquests procediments són eficaços per a decidir, semànticament, si una fórmula és una tautologia o si és, sintàcticament, un teorema del càlcul (sistema axiomàtic.

Com sistema formal, la lògica d'enunciats posseeix també les propietats de consistència i completesa. Posseeix la propietat de consistència, atès que per a qualsevol fórmula vàlida, A, de lògica d'enunciats, és veritat que

si [math]\displaystyle{ \vdash A }[/math], llavors [math]\displaystyle{ \models A }[/math] (Si A és deduïble, A és una conseqüència lògica; si A és un teorema, A és una tautologia)

La qual cosa afirma la seva consistència interna i exclou que sigui possible demostrar A i ¬A, contradictòries entre si. O, cosa que és el mateix, afirma que tots els seus teoremes són vàlids.

És, a més, un sistema formal complet, atès que qualsevol forma vàlida pot ser demostrada dins de la lògica d'enunciats. I, així, per a qualsevol fórmula, A, és veritat que

si [math]\displaystyle{ \models A }[/math], llavors [math]\displaystyle{ \vdash A }[/math] (Si A és una conseqüència lògica, A és deduïble; si A és una tautologia, A és un teorema)

Aquesta és la propietat recíproca, o conversa, de l'anterior, de manera que, en afirmar-se ambdues, les dues propietats anteriors donen lloc a la següent equivalència

[math]\displaystyle{ \vdash A }[/math] si i només si [math]\displaystyle{ \models A }[/math]

El significat d'aquesta equivalència és doble:

1) Totes les seqüències que són deduccions formals són també formalment veritables i, al revés, totes les seqüències formalment veritables són susceptibles d'una demostració formal; i

2) tota deducció és una veritat lògica i totes les veritats lògiques són demostrables; o tot teorema és una tautologia, i tota tautologia és un teorema del sistema.

La lògica d'enunciats és, per tant, un sistema formal consistent, complet i decidible.

(Veure Absorció)

Lògica de predicats

Part de la lògica que té com a objecte d'estudi la conseqüència lògica entre enunciats, quan per a decidir-la no basta considerar l'estructura global dels enunciats, sinó que és necessari conèixer la seva estructura interna. És, en conseqüència, l'estudi de les inferències vàlides que es basen en l'estructura interna dels enunciats. David Hilbert i Wilhelm Ackermann van ser els primers a descriure d'una manera sistemàtica (1928) aquesta part de la lògica, pròpiament anomenada lògica de predicats de primer ordre.

La lògica d'enunciats no pot analitzar satisfactòriament raonaments com els dos següents:

1- Tots els que canten són persones sensibles Raül canta

Per tant Raül és una persona sensible (I que és un raonament correcte)

2) Totes les persones sensibles canten Raül canta

Per tant, Raül és una persona sensible (I que no és un raonament correcte)

En lògica d'enunciats aquests dos raonaments (vàlid el primer, invàlid el segon) tindrien el mateix esquema d'argument: si [math]\displaystyle{ A_1 }[/math] i [math]\displaystyle{ A_2 }[/math], llavors [math]\displaystyle{ B }[/math], la qual cosa no permet decidir quin dels dos és vàlid.

La lògica de predicats, en analitzar l'estructura interna de la frase i en introduir operadors interns, permet diferenciar entre objectes o individus, propietats i relacions.

En «Tot home raona», podem diferenciar l'objecte o individu (el subjecte gramatical) del que es parla, i que aquí es precisa que es tracta de «tots els homes», i la propietat que atribuïm a aquest objecte o individu, que aquí és el predicat «_______ raona». Hi ha predicats que es refereixen a més d'un objecte (com, per exemple, en «_______és el pare de_______» o «_______ està entre_______ i _______», que són relacions).

Una cosa és ser «objecte» o «referent» i una altra de diferent ser «predicat»; els termes que designen objectes són designadors, i els que designen predicats, relators. Així mateix, a l'objecte o referent que pot ocupar l'espai buit « _______ ... » se l'anomena argument; a un argument se li atribueixen predicats, que són propietats (predicats absoluts) o relacions (predicats relatius). Inversament, a les propietats corresponen arguments que són noms, pronoms o objectes i, a les relacions, parelles de noms, o més, segons siguin els predicats diàdics, triàdics, n-àdics (o binaris, ternaris, n-aris, etc.), això és, segons els predicats tinguin dos o més llocs buits.

El llenguatge de la lògica de predicats

La lògica de predicats és un llenguatge formal els enunciats del qual són fórmules amb les quals simbolitza i analitza l'estructura interna de les frases. Aquest llenguatge artificial està format per símbols i fórmules:

• Símbols

Els símbols es componen de: termes, lletres d'enunciat, connectors (o connectives) i quantificadors

1) Termes 1. constants d'individus: a, b, c, ... 2. variables individuals: x, y, z, ... 2) Lletres d'enunciat: P, Q, R, ... 3) Connectives: ¬, ∧,∨ ,→, ↔ 4) Quantificadors: 1. Quantificador universal:∀ (Com en ∀x, que es llegeix: «per a tot x», i equival a «tots») 2. Quantificador existencial: ∃ (Com en ∃x, que es llegeix «hi ha com a mínim un x» i equival a «algun»)

• Fórmules

Les regles de formació de fórmules són les següents:

1) Una lletra de predicat seguida d'un terme és una fórmula (Ex.: Px) 2) Si A i B són fórmules, també ho són ¬A, (A∧B), (A∨B), (A→B) i (A↔B) 3) Si A és una fórmula i x una variable, ∀xA i ∃xA són fórmules 4) Cap altre expressió és una fórmula en lògica de predicats, que no sigui per les regles 1, 2 i 3.

Exemples:

1. Enunciats quantificats.

Exemple

Llenguatge lògic	Enunciat	Llenguatge ordinari
∀x(Rx)	Per a qualsevol x, x és vermell	Tot és vermell
∀x(Rx→Ex)	Per a qualsevol x, si x és vermell, x és extens	Tot el vermell és extens
∀x(Rx↔Ex)	Per a qualsevol x, x és vermell si i només si x és extens	Tot és vermell i extens o ni vermell ni extens
¬∀x(Rx)	No és el cas que, per a tot x, x sigui vermell	No tot és vermell
∀x(¬Rx)	Per a tot x, x no és vermell	Res no és vermell
(¬∀x(Rx→Ex))	No és el cas que, per a tot x, si x és vermell llavors x és extens	No tot el que és vermell és extens
(∀x(Rx→¬Ex))	Per a tot x, si x és vermell, llavors x no és extens	Res vermell és extens
∃x(Rx)	Existeix algun x tal que x és vermell	Alguna cosa és vermella
∃x(Rx∧Ex)	Hi ha algun x tal que x és vermell i extens	Alguna cosa és vermell i extens alhora
¬(∃x(Rx))	No és el cas que existeixi un x tal que x sigui vermell	Res és vermell

2. Enunciats quantificats amb més d'una variable

Exemple

[math]\displaystyle{ \forall{x} \forall{i} (Axy\rightarrow{Gxy}) }[/math]

Per a tot x i per a tot y, si x estima a y, y se sent agraïda a x;

Sempre que una persona n'estima una altra aquesta li ho agraeix.

[math]\displaystyle{ \forall{y} \exists{x}(Gxy) }[/math]

Per tot y hi ha algun x que és la seva ànima bessona;

Tota ànima té la seva ànima bessona.

[math]\displaystyle{ \forall{y} \exists{x}(Axy) }[/math]

Per a tot y hi ha algun x que estima a y;

Tothom estima a algú.

[math]\displaystyle{ \forall{x} \forall{y} (Axy) }[/math]

Per a tot x i per a tot y, x estima a y;

Tothom estima a tothom.

[math]\displaystyle{ \exists{x} \exists{y} (Axy) }[/math]

Per a algun x i per algun y, x estima a y;

Algú estima a algú.

[math]\displaystyle{ \exists{x} \forall{y} (Axy) }[/math]

Per a algun x i per a tot y, x estima a y;

Algú estima a tothom.

[math]\displaystyle{ \forall{x} \forall{y} (¬Axy \longrightarrow{Mxy}) }[/math]

Per a tot x i per a tot y, si no succeeix que x és amic de y, x se sent molest amb y;

Quan no s'és amic d'algú ens és fàcil sentir-nos molests amb ell.

[math]\displaystyle{ ¬ \forall{x} \forall{y} (Axy) }[/math]

No per a tot x i per a tot y, x estima a y;

No tothom estima a tothom.

També la lògica de predicats gaudeix de les propietats de consistència i completesa (en sentit feble: quan tota fórmula vàlida és també un teorema), de manera que tot enunciat o fórmula deduïble és una veritat lògica, i tota veritat lògica és deduïble o derivable; però la lògica de predicats, globalment considerada, no és decidible. A diferència de la lògica d'enunciats, no disposa d'un procediment mecànic, d'un algorisme universal, com són les [#tablasdeverdad taules de veritat], per a decidir si una fórmula qualsevol és universalment vàlida

Exemple

D'un enunciat com [math]\displaystyle{ \forall{x} Px }[/math] pot deduir-se [math]\displaystyle{ \exists{x} Px }[/math], i aquesta deducció pot fer-se sense premisses. Per tant, és possible escriure [math]\displaystyle{ \vdash \forall{x} Px \rightarrow{\exists{x} Px} }[/math] i, per aquesta raó, suposar que [math]\displaystyle{ \models \forall{x} Px \rightarrow{\exists{x} Px} }[/math]

Però aquesta última fórmula, encara que necessàriament veritable, no és una tautologia. La seva veritat es demostra només com a conclusió d'una demostració o derivació.

L'única manera de provar, per a parts determinades d'aquesta lògica, que una fórmula és universalment vàlida, o que un argument és vàlid, és per mitjà d'una deducció. Llavors es compleix que [math]\displaystyle{ A_1, A_2, ... A_n \vdash B }[/math], i si [math]\displaystyle{ \vdash B }[/math], llavors [math]\displaystyle{ \models B }[/math]

I això prova la consistència de la lògica de predicats: tot el que és deduïble és lògicament veritable, o que només les fórmules universalment vàlides són teoremes. I d'aquí, la importància dels mètodes deductius, o càlculs, en lògica de predicats

Sistemes formals de deducció

A part dels sistemes axiomàtics, els sistemes deductius més utilitzats són els arbres lògics (el mateix, substancialment, que en el càlcul d'enunciats) i la deducció natural.

Arbres lògics

Permeten decidir la validesa d'algunes argumentacions de lògica de predicats, atès que, si bé no poden demostrar la consistència de totes les fórmules amb quantificadors, poden demostrar la inconsistència.

Les seves regles són les mateixes del càlcul d'enunciats més quatre pròpies dels quantificadors (vegeu regles).

Veure exemples:

Exemple.

Suposem l'exemple següent:

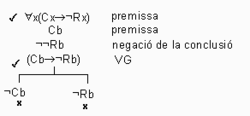
La crítica que procedeix d'una certa necessitat psicològica de fer-la en aquells que la fan no mereix una resposta racional. Quan la gent es queixa que la psicoanàlisi sosté afirmacions bàrbares i arbitràries sobre la sexualitat infantil, la seva crítica procedeix de determinades exigències psicològiques d'aquesta mateixa gent. Per tant la crítica que es basa a dir que la psicoanàlisi sosté afirmacions bàrbares i arbitràries sobre la sexualitat infantil no mereix una resposta racional.

(Text arreglat, procedent de la Conferència XXXIV de Noves aportacions a la psicoanàlisi, en S. Freud, Obres completes, 3 vols., Biblioteca Nova, Madrid 1968, vol. II, p. 943-953).

Sigui la següent interpretació:

Cx: x és una crítica que procedeix d'una certa necessitat psicològica de fer-la en aquells que la fan.

Rx: x mereix una resposta racional.

b: la queixa que la psicoanàlisi sosté afirmacions bàrbares i arbitràries sobre la sexualitat infantil.

Transcrites com a fórmules, tenim el següent raonament:

[math]\displaystyle{ [ \forall{x} (Cx\rightarrow{¬Rx})\wedge Cb]\rightarrow{¬Rb} }[/math]

La seva prova mitjançant un arbre molt breu. Només utilitza una regla (la VG):

Exemple pres de W. Hodges, Logic, Penguin Books, Londres 1991, p.230-231

Exemple.

Tot el que agrada és il·legal, o immoral o engreixa. Prendre's un gelat és agradable. Prendre's un gelat no és il·legal ni immoral. Per tant, prendre's un gelat engreixa.

Deducció natural

Utilitza les mateixes regles del càlcul de lògica d'enunciats més quatre regles bàsiques pròpies del càlcul de predicats, i algunes derivades (vegeu regles).

Exemples:

Exemple 1

• Penso, i tot el que pensa existeix.
• Per tant, jo existeixo.

[math]\displaystyle{ Pa, \forall x(Px \rightarrow Ex), \vdash Ea\\ }[/math]

[math]\displaystyle{ 1. Pa ~~~~~~~~~~~~~~~~~~~~~Premissa\\ 2. \forall x (Px \rightarrow Ex)~~~~~~Premissa\\ 3. Pa \rightarrow Ea~~~~~~~~~~~~EG2\\ 4. Ea ~~~~~~~~~~~~~~~~~~~~MP 1,3\\ }[/math]

Exemple 2

• La primavera la sang altera
• Per tant, atès que som a la primavera, a Anna la sang se li altera

[math]\displaystyle{ Pa, \forall x Cx, P \vdash Ea\\ }[/math]

[math]\displaystyle{ 1. P \rightarrow (\forall x Cx) ~~~~~~~~~~~~Premissa\\ 2. P ~~~~~~~~~~~~~~~~~~~~~Premissa\\ 3. \forall x Cx ~~~~~~~~~~~~~~~~MP 2,1\\ 4. Ea ~~~~~~~~~~~~~~~~~~~EG 3\\ }[/math]

Exemple 3

• Totes les teories científiques es recolzen en l'experiència,
• però algunes teories psicològiques no es recolzen en cap experiència.
• Per tant, algunes teories psicològiques no són científiques.

[math]\displaystyle{ 1.\forall c(Cx\rightarrow Ex)~~~~Premissa\\ 2.\exists x(Px\wedge \neg Ex)~~~~Premissa\\ 3.Pa\wedge \neg Ea)~~~~EP2\\ 4.Ca\rightarrow Ea ~~~~EG1\\ 5. \neg Ea \rightarrow \neg Ca ~~~~Cp4\\ 6.\neg Ea ~~~~EC3\\~ 7. \neg Ca ~~~~MP 5,6\\ 8. Pa ~~~~EC 3\\ 9.Pa\wedge \neg Ca~~~~IC 7,8\\ 10. \exists x(Px \wedge \neg Cx )~~~~IP 9\\ }[/math]

Lògica de classes

La lògica que tracta de les classes i dels membres de les classes. S'identifica amb la lògica de predicats monàdics, i en ella es distingeixen dues parts: l'àlgebra de classes i la lògica de classes pròpiament dita.

L'àlgebra de classes pot considerar-se com una interpretació extensional de la lògica d'enunciats, on les lletres no signifiquen enunciats, sinó classes, això és, el conjunt d'objectes o individus que tenen la mateixa propietat: una classe és l'extensió d'un predicat. L'expressió «x és pianista» s'interpreta com a «x és membre de la classe de pianistes» = Px. Tot objecte que tingui la propietat de «ser pianista» pertany a aquesta classe. La classe de tots aquests objectes amb aquesta propietat s'escriu amb l'operador d'abstracció

[math]\displaystyle{ P=_{df} }[/math]{[math]\displaystyle{ {\hat{x} Px} }[/math]} i es llegeix "la classe de tots els x tals que x és P".

Es distingeix entre classes finites (per exemple, els dies de la setmana) i infinites (per exemple, la sèrie de nombres naturals); classes unitàries, amb un únic element (per exemple, el nombre B); classe buida (per exemple, una setmana de només tres dies) i classe universal o univers de discurs, representada per la classe on cobra sentit parlar d'altres classes i les seves propietats; parlar d'«atletes» i de les seves «marques» té sentit en un univers d'homes i dones.

Es distingeixen, així mateix, operacions entre classes i relacions entre classes. El resultat d'aquestes últimes són enunciats sobre classes; el resultat de les primeres és una nova classe.

Operacions entre classes:

Són les classes produïdes pels operadors de classe «productor», «sumador» i «complementador»

[math]\displaystyle{ \cap, \cup, \bar{} }[/math]

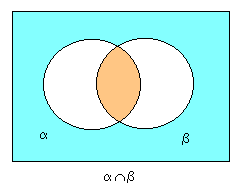
La intersecció , multiplicació lògica, o classe producte, [math]\displaystyle{ A\cap B }[/math] està formada pels individus que pertanyen, alhora, a A i a B. Així, «filòsofs catalans» és la intersecció entre la classe de «filòsofs» i la de «catalans».

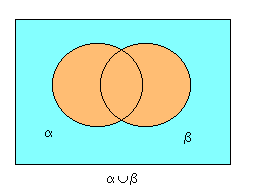
La unió , o suma lògica, o classe summa, [math]\displaystyle{ A\cup B }[/math] és la classe formada pels individus que pertanyen a una de les dues classes o a ambdues. La classe del «personal sanitari» està constituïda per metges, personal A.T.S. i per aquells –si n'hi ha– que són ambdues coses alhora.

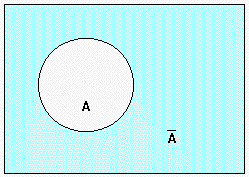
La classe complement o complementària de [math]\displaystyle{ A \overline{A} }[/math] és aquella a la qual pertanyen els elements que no pertanyen a A: la classe complement dels dies festius d'un mes són tots els altres dies laborables.

Classes disjuntes són aquelles la intersecció de les quals és buida. La classe dels «homes» és disjunta de la dels «animals que volen», perquè «Cap home vola». Per això, els enunciats categòrics de forma I poden escriure's com

[math]\displaystyle{ A\cap B = 0 }[/math]<c/enter>

De la mateixa manera que els enunciats categòrics de forma A poden escriure's com una classe disjunta d'una classe A i la classe complement d'una altra

[math]\displaystyle{ A\cap \overline{B} = 0 }[/math]

En canvi, els enunciats categòrics particulars afirmen que dues classes no són disjuntas, una respecte d'una altra. Així, «alguns mamífers viuen en el mar», enunciat de tipus I, pot escriure's com

[math]\displaystyle{ A\cap B \neq 0 }[/math]

que afirma que la intersecció de A i B no és buida. Pel mateix, un enunciat de tipus O, com «algunes expressions no són afortunades», s'escriu com una intersecció no buida entre una classe, A, i la classe complement de B

[math]\displaystyle{ A\cap \overline{B} \neq 0 }[/math]

Relacions entre classes

Enunciats sobre classes, construïts amb les constants d'enunciats de classe [math]\displaystyle{ "\subset, = " }[/math]

La inclusió de classes, que s'escriu

[math]\displaystyle{ A\subset B }[/math]

es llegeix com a «A està continguda en B» i es defineix afirmant que si alguna cosa pertany a A, pertany també a B, raó per la qual A és una subclasse de B. L'enunciat «els catalans són europeus» inclou la classe «catalans» en la classe dels «europeus», sent la primera una subclasse de la segona.

Tota classe té la propietat reflexiva (s'inclou a si mateixa) i la transitiva (si A està inclosa en B i aquesta en C, A està inclosa en C).

La igualtat entre classes, que s'escriu

[math]\displaystyle{ A = B }[/math]

i es llegeix «la classe A és idèntica a B», afirma d'elles que l'una i l'altra tenen els mateixos elements. Així, per exemple, la classe dels nombres naturals parells és igual a la classe de nombres divisibles per dos.

L'ús conjunt i combinat dels operadors de classe i les constants d'enunciats de classes (més les constants de classe, com a conjunt buit i classe universal, a més dels parèntesis) permet formar enunciats de lògica de classes. Aquells enunciats de classes que són universalment veritables, o que són tautològics constitueixen les lleis del càlcul de lògica de classes.

L'àlgebra de Boole és un càlcul basat en només dues operacions de lògica de classes: la intersecció i la unió de classes, i el recurs, a més, a la classe complement.

Lògica de relacions

Desenvolupament de la lògica de predicats que permet l'estudi de la deducció en raonaments que utilitzen enunciats amb predicats poliàdics, o predicats amb més d'un lloc, amb els quals s'expressen relacions entre dues o més individus (binàries, ternàries, n-àries). Aquesta lògica permet tractar arguments com:

A qui li agrada París li agrada també Roma. A Anna li agrada París

Només ciutats belles carregades d'història li agraden a Anna

_______________________________________________________

Per tant Roma és una bella ciutat carregada d'història

On «x agrada a y» és una relació.

O el conegut d'Augustus de Morgan:

Un cavall és un animal

________________________________________________

Per tant, el cap d'un cavall és el cap d'un animal

(on «x és el cap de i» és una relació).

Vegeu també: història de la lògica, lògica simbòlica / lògica matemàtica, sil·logística