Pitagorisme
De Wikisofia
Ampli moviment filosòfic d'origen presocràtic basat en les doctrines atribuïdes a Pitàgores de Samos i els seus deixebles més immediats. El pitagorisme pròpiament dit és el moviment d'investigació filosòfica, matemàtica i mística desenvolupat durant el segle V aC pels deixebles de Pitàgores, encara que com a tal moviment es va iniciar ja a partir de la primitiva secta filosòfica-mística-religiosa fundada per Pitàgores al segle VI aC i, posteriorment, va continuar durant diversos segles sota la forma de neopitagorisme.
El principal problema que es presenta per a l'estudi del pitagorisme és el caràcter secret i tancat de la primitiva secta pitagòrica, agreujat pel fet que Pitàgores mateix, o bé no va escriure cap obra (les que se li van atribuir, conegudes com Els tres llibres, i els Versos àuris, són obres apòcrifes del segle I aC o del segle I dC), o bé no es conserven els seus escrits (Diògenes Laerci esmenta diversos escrits de Pitàgores, veg. text). De fet, els primers escrits pitagòrics coneguts i importants són obra de Filolau. Per això és difícil assenyalar els límits entre els seus ensenyaments i les doctrines considerades generalment com a pitagòriques. Aquesta dificultat s'accentua encara més si tenim en compte que Pitàgores mateix va ser abans de res el fundador d'una secta místic-religiós-política d'inspiració òrfica en la qual la investigació matemàtica i filosòfica i música estava al servei de les creences religioses. Com en tota secta, estava molt estesa la tendència a venerar al fundador, i fins i tot a atribuir-li tots els descobriments i totes les doctrines. A més, el caràcter secret i esotèric d'aquesta secta impedia que les seves doctrines fossin exposades i difoses al públic no iniciat (Hipàs va ser perseguit i assassinat per membres de la secta per haver desvelat un secret de geometria), de manera que això accentua encara més la dificultat de destriar què es deu a Pitàgores i què és obra dels anomenats pitagòrics. Pel que sembla, es deu a Pitàgores mateix les doctrines religioses de la immortalitat i de la transmigració de les ànimes, el descobriment de les relacions entre l'harmonia musical, els concordes i les proporcions numèricament expressables, així com els inicis de la matemàtica especulativa i la cosmologia filosòfica.
L'escola pitagòrica va subsistir durant molt temps, i en la seva llarga tradició es barregen diverses doctrines i teories, algunes de les quals poden haver estat iniciades en l'època mateixa de Pitàgores, però unes altres són, amb tota seguretat, molt posteriors. Si a això s'hi afegeix que moltes de les doctrines pitagòriques ens són conegudes a través del moviment neopitagòric, i que en el període hel·lenístic es van escriure gran quantitat de textos apòcrifs atribuïts a Pitàgores, es veu la gran dificultat d'un tractament rigorós del pitagorisme. Per això, molts autors consideren que, deixant apart el neopitagorisme, ha d'entendre's per pitagorisme el conjunt del pensament d'aquells que Aristòtil anomena pitagòrics, reconeixent en aquest autor l'autoritat i el coneixement suficient per a cenyir-nos a la descripció que ell ens ofereix.
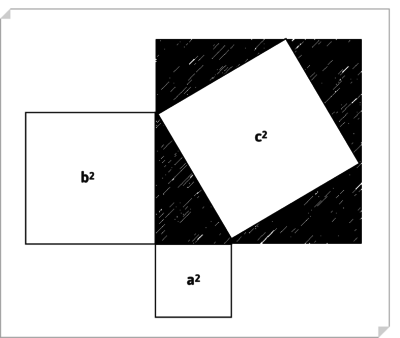
Així, a més de la filosofia atribuïda a Pitàgores, el pitagorisme seria el conjunt de doctrines d'autors com Hipàs de Metapont (al que alguns atribueixen el descobriment de l'anomenat «teorema de Pitàgores»), Ecfant, Hicetes, Filolau, Arquites de Tàrent i, encara que separant-se una mica del conjunt dels altres autors, Alcmeó de Crotona. En el seu conjunt, aquests pensadors segueixen la tendència mística i religiosa general del pensament de Pitàgores, advoquen per una vida ascètica i per ritus de purificació, entenent el mateix conrreu de les matemàtiques com a camí de purificació moral. Conceben la naturalesa a partir de relacions numèriques i, a més, el nombre és per a ells el principi o ἀρχή (arkhé) i la matèria de les coses.
La concepció pitagòrica dels nombres està fortament marcada pel misticisme, i els consideren tant responsables de l'harmonia que governa el cosmos (ϰόσμος), com elements explicatius de les qualitats morals. De la mateixa manera que l'harmonia musical (expressable mitjançant relacions numèriques) implica la unitat d'una multiplicitat de sons separats entre si per intervals definits, conceben el conjunt del cosmos com un tot ordenat per relacions numèriques que formen l'harmonia del cosmos. Això és així perquè la naturalesa mateixa és barreja d'unitat i multiplicitat, del determinat i l'indeterminat, del finit i l'infinit, ja que tot està regit pels mateixos principis del límit i l'il·limitat que regeixen els nombres. Així, tot fenomen és expressió sensible de les raons matemàtiques (veg. citació d'Aristòtil).
Al seu torn, els elements dels nombres són el limitat i l'il·limitat (l'imparell i el parell respectivament). ja que l'U està compost de tots dos, atès que, segons els pitagòrics, és simultàniament parell i imparell, és el fonament últim de caràcter diví. Tots els nombres neixen de l'U i els seus principis (el limitat i il·limitat) generen una sèrie de principis d'oposats (veg. citació d'Aristòtil) que són els següents:
| ________________ | Límit | Il·limitat |
| Imparell | Parell | |
| Unitat | Pluralitat | |
| Dret | Esquerre | |
| Mascle | Femella | |
| En repòs | En moviment | |
| Recte | Corb | |
| Llum | Foscor | |
| Bo | Dolent | |
| Quadrat | Rectangle |
(Alguns autors, com Guthrie, per exemple, han assenyalat les semblances entre aquesta taula pitagòrica dels oposats amb la de la concepció del Yin i el Yang, veg. citació).
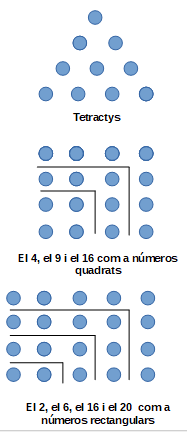
En la seva concepció política, de caràcter elitista i aristocratitzant, conceben la societat de savis (que segueix l'estructura de la mateixa secta pitagòrica) com el model de la societat ideal. La seva concepció de l'ètica està dominada pel dualisme òrfic i per la creença en la transmigració de les ànimes o metempsicosi. Defensen un model cosmològic segons el qual la terra no és el centre del cosmos, sinó que gira, igual que tots els altres cossos celestes, inclòs el sol, al voltant d'un foc central. Explicant aquest foc central, més tots els altres astres coneguts, formen un conjunt de nou cossos celestes. Però com que consideren que el 10 és el nombre perfecte (1+2+3+4=10, i els quatre primers nombres són els que determinen les concordances musicals), al qual representen com un triangle a què anomenen tetraktys, inclouen en el seu model cosmològic un desè cos celeste, l'antiterra, que és invisible per a nosaltres perquè està oposada a la terra. D'altra banda, les distàncies entre les òrbites d'aquests cossos celestes, i el moviment d'aquests, forma una harmonia còsmica o música de les esferes.
La figura de la divina tetraktys era utilitzada pels pitagòrics com a base sobre la qual pronunciaven els seus juraments. A més van descobrir diverses propietats dels nombres. Així, per exemple, van anomenar nombres quadrats a aquells que podien disposar-se formant aquesta figura geomètrica, com el 4, 9, 16, 25, etc. És a dir: [math]\displaystyle{ 2^2, 3^2, 4^2, 5^2, etc. }[/math] Mentre que nombres com el 2, 6, 12, 20, etc. eren anomenats nombres rectangulars.
Aquest moviment va tenir una gran influència en l'antiguitat, fonamentalment sobre Plató, que va ser influït per Filolau i, sobretot, per Arquites de Tàrent, i les orientacions pitagòriques del qual són especialment visibles en el Timeu (veg. textos ), i sobre molts dels seus seguidors (que van formar la teoria de les idees-nombres). Però el pitagorisme va exercir també una perdurable influència en la filosofia del Renaixement, en les concepcions místiques sobre els nombres i en la tradició cabalista.
Una de les principals crisis amb les quals es va haver d'enfrontar l'escola pitagòrica va ser deguda, precisament, al descobriment del teorema de Pitàgores, ja que manifestava l'existència de nombres incommensurables (com la diagonal d'un quadrat i el seu costat). L'existència d'aquestes magnituds va suscitar un fort debat en el si de l'escola i va posar de manifest el problema del continu. A partir d'aquest moment l'aritmètica i la geometria van seguir diferents camins, i el problema mateix del continu va originar una important font de reflexió filosòfica que va ser explotada per l'escola eleàtica de Parmènides i Zenó d'Elea.
Els pitagòrics, a més de les seves investigacions, van desenvolupar una intensa activitat política que els va conduir a posseir el poder en moltes polis de la Magna Grècia. Cap a l'any 450 aC, i davant la revolució democràtica que es va produir, molts d'ells van haver de fugir i anar-se'n a la Grècia continental. A més de l'escola pitagòrica de Crotona van destacar les escoles de Fliunt, Locri (amb Timeu), Tàrent (amb Arquites), Tebas (amb Filolau, Simmias i Cebes) i Siracusa (amb Ecfant i Hicet).
Veg. mathema, Similia_similibus_percipiuntur.