Diferència entre revisions de la pàgina «Funció»
De Wikisofia
m (Text de reemplaçament - " la hi " a " se la ") |
m (Text de reemplaçament - "File:i" a "File:e") |
||
| Línia 9: | Línia 9: | ||
<center>'''veure exemple ↓'''</center> | <center>'''veure exemple ↓'''</center> | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| − | <center>[[File: | + | <center>[[File:e1658-1.gif]]</center> |
</div></div> | </div></div> | ||
| Línia 21: | Línia 21: | ||
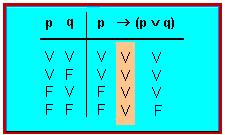
Així, per a l'enunciat <math>p \rightarrow{(p \vee q)}</math> la taula de veritat és | Així, per a l'enunciat <math>p \rightarrow{(p \vee q)}</math> la taula de veritat és | ||
| − | <center>[[File: | + | <center>[[File:e1658-2.gif]]</center> |
[[Recurs:exemple taula veritat 1]] | [[Recurs:exemple taula veritat 1]] | ||
Revisió del 15:40, 25 abr 2015
(del llatí functio, execució, compliment, de fungor, duc a terme)
En sentit general derivat de la seva etimologia, allò per el que alguna cosa o algú serveix a manera de causa instrumental, com quan es diu que algú o alguna cosa compleix o no amb la seva funció, o es parla de les diverses funcions del llenguatge o de les quals compleixen els mitjans de comunicació. L'ús del terme és més adequat en biologia i aritmètica. En biologia, la funció es refereix al paper que exerceix una part (membre o característica) dins del procés evolutiu de tot l'organisme, preferentment la nutrició, la relació i la reproducció.
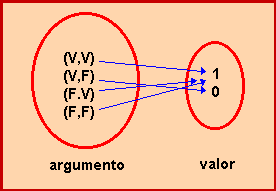
En matemàtiques, lingüística i lògica una funció és una relació entre dos elements, x, i, tal que a cada valor de x (anomenat argument de la funció) li correspon un valor de i (anomenat valor de la funció); al conjunt de valors de la variable x se l'anomena domini de la funció, i al conjunt de valors i de la funció se l'anomena rang o codominio. Rep també el nom de aplicació, quan és l'assignació d'un o diversos membres d'un conjunt X a un únic membre del conjunt I (correspondència unívoca);
Les connectives de la lògica d'enunciats es defineixen com funcions veritatives: coneixent el valor dels enunciats simples p i q, podem conèixer el valor dels enunciats composts [math]\displaystyle{ p\vee q }[/math], o [math]\displaystyle{ p\rightarrow{q} }[/math]
Les taules de veritat lògiques posen de manifest com les connectives són símbols veritativo-funcionals, o símbols que designen una funció veritativa entre un enunciat compost i els valors de veritat:
Així, per a l'enunciat [math]\displaystyle{ p \rightarrow{(p \vee q)} }[/math] la taula de veritat és
Gottlob Frege va tractar els conceptes i els predicats com a funcions.
En sociologia, funció pot ser la relació matemàtica que, ajustant-se a una metodologia científica, s'estableix entre dos elements de l'entramat social. Així, Durkheim estudia el suïcidi posant-ho en relació (en raó inversa) amb la integració d'un individu en el seu grup. En un sentit més específic, justifica una institució social per (en funció de) les conseqüències benèfiques que aporta per al manteniment de tot el sistema social. Aquesta aplicació del concepte biològic de funció al sistema social, considerat com un organisme, es remunta a Herbert Spencer (1820-1903). Es parla de eufunciones i disfuncions, segons aquestes conseqüències siguin positives o negatives. En aquest sentit es pot parlar de la funció (positiva) que exerceix, posem per cas, la institució de l'ensenyament en la societat i així també pot parlar-se de la funció de la família o l'escola en la societat, entenent que aquestes institucions exerceixen una funció, això és, una necessitat vital per a la societat. A l'orientació general en sociologia (i també en antropologia) que explica l'existència de les institucions socials com a funcions que satisfan necessitats vitals de la societat entesa com un organisme, se la denomina funcionalisme.