Diferència entre revisions de la pàgina «Modus ponendo tollens»
De Wikisofia
(Es crea la pàgina amb «{{ConcepteWiki}} Expressió llatina, que significa «manera de negar afirmant», amb la qual en lògica es caracteritza a l`argument la forma del qual...».) |
|||
| (4 revisions intermèdies per 2 usuaris que no es mostren) | |||
| Línia 1: | Línia 1: | ||
{{ConcepteWiki}} | {{ConcepteWiki}} | ||
| − | Expressió llatina, que significa «manera de negar afirmant», amb la qual en lògica es caracteritza a l | + | Expressió llatina, que significa «manera de negar afirmant», amb la qual en lògica es caracteritza a l'[[argument |argument]] la forma del qual és: «P o Q; P, per tant no Q», i en el qual la «o», o la [[disjunció|disjunció]], s'interpreta en sentit exclusiu. |
<div class='mw-collapsible mw-collapsed'> | <div class='mw-collapsible mw-collapsed'> | ||
| − | <center>''' | + | <center>'''veg. exemple ↓'''</center> |
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
:Culpable o innocent | :Culpable o innocent | ||
:No és culpable | :No és culpable | ||
:______________ | :______________ | ||
| − | : | + | :Per tant és innocent |
Revisió de 18:56, 1 maig 2020
Expressió llatina, que significa «manera de negar afirmant», amb la qual en lògica es caracteritza a l'argument la forma del qual és: «P o Q; P, per tant no Q», i en el qual la «o», o la disjunció, s'interpreta en sentit exclusiu.
- Culpable o innocent
- No és culpable
- ______________
- Per tant és innocent
És una forma de sil·logisme disjuntiu; en lògica d'enunciats s'utilitza la forma de disjunció corresponent a la «o» inclusiva, o modus tollendo ponens, o simplement sil·logisme disjuntiu, amb el qual no ha de confondre's.
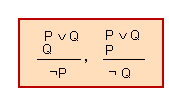
En lògica d'enunciats, li correspon la llei lògica